学术报告（一）

报告题目：Standing waves for quasilinear Schrodinger equations with indefinite potentials

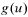报告摘要：We consider quasilinear Schrödinger equations in of the form    where is 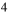-superlinear. Unlike all known results in the literature, the Schrödinger operator 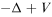is allowed to be indefinite, hence the variational functional does not satisfy the mountain pass geometry. By a local linking argument and Morse theory, we obtain a nontrivial solution for the problem. In case that is odd, we get an unbounded sequence of solutions.

报告人：刘轼波  厦门大学教授、博士生导师

报告时间：6月11日下午3：00-4：00

报告地点：金沙集团wwW3354CC学术楼报告厅（304）

学术报告（二）

报告题目：欧式空间之间的满射、重积分换元公式和Brouwer不动点定理

摘要：给出了m-重积分换元公式的新的证明。它比传统的证明更为简单，而且作为其副产品能得到m-维的Brouwer不动点定理。证明中用到线性代数中的Cauchy-Binet公式以及行列式按行展开等结果，很好地表现了代数对分析的作用；把经典结论“设 R^n 到自身的映射 f 的 Jacobi 行列式处处非零，并且 |x| 趋于无穷时 |f(x)| 趋于无穷，则 f 是满射”推广到很一般的情形，作为推论得到代数基本定理，以及看起来有些惊人的结论：紧流形上的向量值函数必有无穷多个临界点。

报告人：刘轼波  厦门大学教授、博士生导师

报告时间：2018年6月11日下午4:30-5:20

报告地点：金沙集团wwW3354CC201教室

报告人简介：刘轼波, 男，厦门大学数学系教授、博士生导师、数学系副主任。主要研究领域是非线性泛函分析、非线性偏微分方程的变分方法及其应用。2003年中国科学研究院数学与系统科学研究院数学所获得博士学位, 2005年北京大学数学研究所博士后出站，2008年任汕头大学教授，2011年任厦门大学教授。先后主持国家自然科学基金青年项目和面上项目多项, 以及福建省杰出青年基金项目。2013年入选意大利国际理论物理中心(ICTP)协联成员, 2017年受国家留学基金委资助到美国圣母大学访问一年。