报告题目：Non-degeneracy and new existence of bubble solutions for the Hénon-type equation with critical growth

主讲人：刘婷博士（清华大学）

报告时间：5月5日（周四）10:00-11:00

报告地点：腾讯会议 ID: 752-424-076

主办单位：金沙集团wwW3354CC

报告摘要：

We consider the following Hénon-type equation with critical growth:

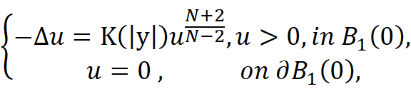
where 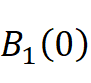 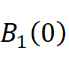is the unit ball in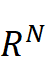 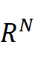, K : [0, 1] →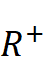 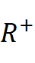 is a bounded function. We prove a non-degeneracy result of the bubbling solutions constructed in [24] via the local Pohozaev identities for N ≥ 5. Then, by using reduction arguments combine with delicate estimates for the modified Green function and the error, we prove the new existence of infinitely many non-radial solutions, whose energy can be arbitrarily large.

[24] J. Wei, S. Yan: Infinitely many nonradial solutions for the Hénon equation with critical growth. Rev. Mat. Iberoam. 29 (2013), no.3, 997-1020.

报告人简介：

刘婷博士，2017 年 7 月于北京师范大学金沙集团wwW3354CC数学与应用数学专业获得理学学士学位；2017 年 9 月免试进入清华大学数学科学系攻读理学博士至今，师从郭玉霞教授。主要从事非线性泛函分析及其在偏微分方程中的应用等方面的研究工作，近三年在 Calc. Var. Partial Differential Equations、 Discrete Contin. Dyn. Syst.、Adv. Nonlinear Stud.、 Ann. Mat. Pura Appl.、 Manuscripta Math.及 Math. Nachr.等国际知名期刊上发表论文近10篇。